DETERMINAÇÃO DE MOMENTOS EM LAJES MACIÇAS

Dimensionar lajes maciças utilizando tabelas é uma abordagem prática para engenheiros e projetistas, pois facilita a determinação dos esforços internos, como momentos fletores e cortantes, nas lajes de concreto armado. A solução em séries para determinação dos momentos atuantes, desenvolvida por Bares e adaptada por L.M. Pinheiro e P.R. Wolfensberger, será apresentada a seguir. No entanto, há também outros trabalhos igualmente conhecidos, como as tabelas de Czerny e Marcus.

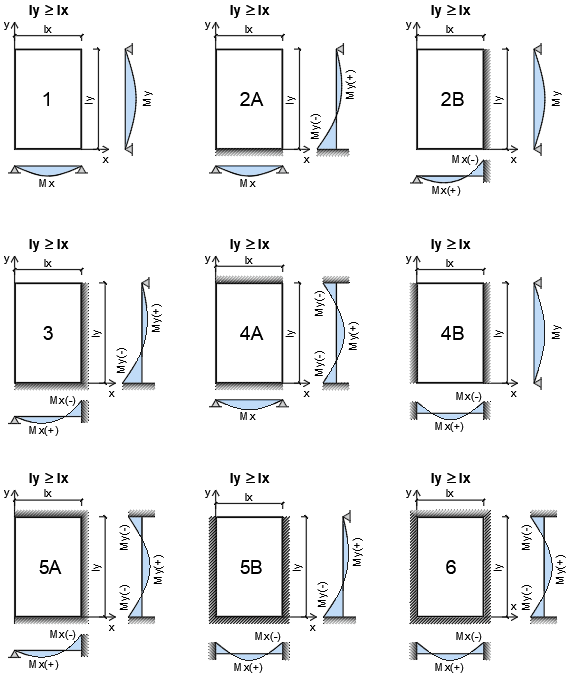
desenho que ilustra as condições de vinculação — Condições de vinculação

A partir da determinação das dimensões da laje retangular (calculando a relação entre as dimensões da laje, $\lambda = \frac{l_{y}}{l_{x}}$ ) e condições de vinculação de seus apoios, conforme os modelos propostos na imagem acima, utilizam-se tabelas para determinar os coeficientes ( $\mu_{x},\mu_{y},\mu^{'}_{x},\mu^{'}_{y}$ ) para o cálculo dos momentos fletores máximos.

$M_{max} = \mu \cdot \frac{p\cdot l_{x}^{2}}{100}$

Sendo $l_{x}$ o menor vão da laje.

A seguir, serão apresentados três exemplos práticos sobre a utilização das tabelas de Bares para a determinação dos momentos fletores máximos em lajes retangulares.

EXEMPLO 1

Supondo uma laje retangular de concreto armado com dimensões de 300 cm x 450 cm, engastada em seu bordo 2 e simplesmente apoiada nos bordos 1, 3 e 4, conforme imagem abaixo, calcule os momentos fletores atuantes nas duas direções. Considar laje com espessura igual a 12 cm, carga de revestimento igual a g=150kg/m² e carga acidental (utilização) igual a q=200kg/m².

desenho da laje de exemplo utilizada no cálculo — Exemplo de laje

1º PASSO: Cálculo de $\lambda$

Para determinar o valor de $\lambda$ , precisamos definir $l_{x}$ e $l_{y}$ .

$l_{x}$ será sempre a menor das dimensões a laje, portanto, $l_{x} = 300 cm$ .
$l_{y} = 450 cm$ .

$\lambda = \frac{l_{y}}{l_{x}} = \frac{450}{300} = 1,5$

2º PASSO: Obter os valores dos coeficientes em tabela

A partir das condições da vinculação da laje e do valor de $\lambda$ , podemos utilizar as tabelas para obter os coeficientes que serão utilizados para o cálculo dos momentos fletores. Observe que a laje presente no exemplo 1 apresenta as mesmas condições de vinculação do Caso 2B, conforme tabela abaixo.

tabela com os coeficientes para determinar os momentos fletores atuantes — Tabela: coeficientes

A partir do valor de $\lambda = 1,5$ e observando que se trata do Caso 2B, obtemos na tabela acima os coeficientes:

$\mu_{x} = 5,24$
$\mu^{'}_{x} = 11,09$
$\mu_{y} = 2,12$

3º PASSO: Cálculo do carregamento atuante

Como definido anteriormente, serão consideradas as cargas de revestimento igual a g=150kg/m² e carga acidental (utilização) igual a q=200kg/m². Além disso, temos o peso próprio definido como:

$P_{p} = e_{laje} \times \gamma_{concreto} = e_{laje} \times 2500 kg/m^{3} = 0,12 \times 2500 = 300kg/m^{2}$

Temos, portanto, que a carga total é: $P = P_{p} + g + q = 300 + 150 + 200 = 650 kg/m^{2}$

Ou: $P \cong 6,5 kN/m^{2}$

4º PASSO: Cálculo dos momentos fletores (valores característicos por faixa de metro)

O cálculo dos momentos pode ser feito através da equação:

$M_{max} = \mu \cdot \frac{p\cdot l_{x}^{2}}{100}$

Portanto:

Momento positivo (+) em X:

$M_{x}^{+} = \mu_{x} \cdot \frac{p\cdot l_{x}^{2}}{100}$

$M_{x}^{+} = 5,24 \cdot \frac{6,5\cdot 3^{2}}{100} \cong 3,06 kN.m/m$

Momento negativo (-) em X:

$M_{x}^{-} = \mu^{'}_{x} \cdot \frac{p\cdot l_{x}^{2}}{100}$

$M_{x}^{-} = 11,09 \cdot \frac{6,5\cdot 3^{2}}{100} = 6,49 kN.m/m$

Momento positivo (+) em Y:

$M_{y}^{+} = \mu_{y} \cdot \frac{p\cdot l_{x}^{2}}{100}$

$M_{y}^{+} = 2,12 \cdot \frac{6,5\cdot 3^{2}}{100} = 1,24 kN.m/m$

imagem demonstra o momento atuante calculado para as duas direções — Momento atuante: exemplo 1

A partir dos momentos fletores atuantes, é possível dimensionar as armaduras necessárias.

EXEMPLO 2

Supondo uma laje retangular de concreto armado com dimensões de 300 cm x 450 cm, engastada em seus bordos 1 e 3 e simplesmente apoiada nos bordos 2 e 4, conforme imagem abaixo, calcule os momentos fletores atuantes nas duas direções. Considar laje com espessura igual a 12 cm, carga de revestimento igual a g=150kg/m² e carga acidental (utilização) igual a q=200kg/m².

Note que as dimensões e os carregamentos são os mesmos apresentados no EXEMPLO 1, portanto, temos que o valor de $\lambda$ e o carregamento total $P = P_{p} + g + q$ são:

$\lambda = \frac{l_{y}}{l_{x}} = \frac{450}{300} = 1,5$

$P \cong 6,5 kN/m^{2}$

A partir das condições da vinculação da laje e do valor de $\lambda$ , podemos utilizar a tabela abaixo para obter os coeficientes que serão utilizados para o cálculo dos momentos fletores. Observe que a laje do exemplo em questão apresenta as mesmas condições de vinculação do Caso 4A.

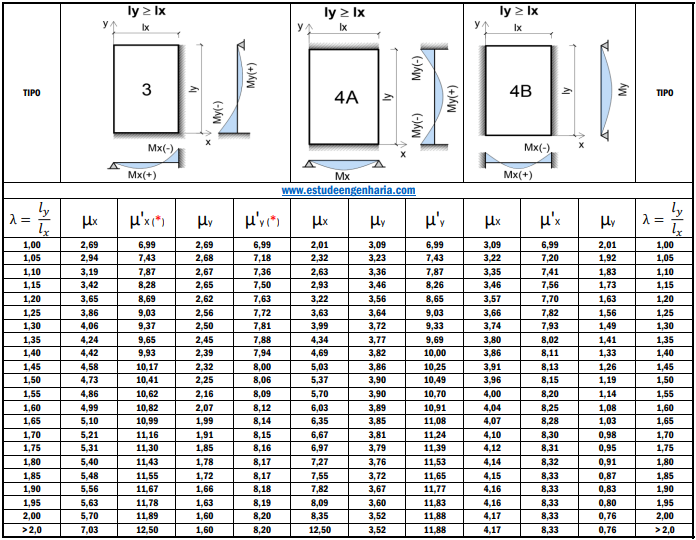
Temos, portanto, os coeficientes:

$\mu_{x} = 5,37$
$\mu_{y} = 3,90$
$\mu^{'}_{y} = 10,49$

Momento positivo (+) em X:

$M_{x}^{+} = \mu_{x} \cdot \frac{p\cdot l_{x}^{2}}{100}$

$M_{x}^{+} = 5,37 \cdot \frac{6,5\cdot 3^{2}}{100} \cong 3,14 kN.m/m$

Momento positivo (+) em Y:

$M_{y}^{+} = \mu_{y} \cdot \frac{p\cdot l_{x}^{2}}{100}$

$M_{y}^{+} = 3,90 \cdot \frac{6,5\cdot 3^{2}}{100} = 2,28 kN.m/m$

Momento negativo (-) em Y:

$M_{y}^{-} = \mu^{'}_{y} \cdot \frac{p\cdot l_{x}^{2}}{100}$

$M_{y}^{-} = 10,49 \cdot \frac{6,5\cdot 3^{2}}{100} = 6,14 kN.m/m$

A partir dos momentos fletores atuantes, é possível dimensionar as armaduras necessárias.

EXEMPLO 3

Supondo uma laje retangular de concreto armado com dimensões de 300 cm x 450 cm, engastada em seus bordos 1, 2 e 3 e simplesmente apoiada no bordo 4, conforme imagem abaixo, calcule os momentos fletores atuantes nas duas direções. Considar laje com espessura igual a 12 cm, carga de revestimento igual a g=150kg/m² e carga acidental (utilização) igual a q=200kg/m².

Note que as dimensões e os carregamentos são os mesmos apresentados no EXEMPLO 1, portanto, temos que o valor de $\lambda$ e o carregamento total $P = P_{p} + g + q$ são:

$\lambda = \frac{l_{y}}{l_{x}} = \frac{450}{300} = 1,5$

$P \cong 6,5 kN/m^{2}$

Temos, portanto, os coeficientes:

$\mu_{x} = 4,23$
$\mu^{'}_{x} = 9,44$
$\mu_{y} = 2,43$
$\mu^{'}_{y} = 7,91$

Momento positivo (+) em X:

$M_{x}^{+} = \mu_{x} \cdot \frac{p\cdot l_{x}^{2}}{100}$

$M_{x}^{+} = 4,23 \cdot \frac{6,5\cdot 3^{2}}{100} \cong 2,47 kN.m/m$

Momento negativo (-) em X:

$M_{x}^{-} = \mu^{'}_{x} \cdot \frac{p\cdot l_{x}^{2}}{100}$

$M_{x}^{-} = 9,44 \cdot \frac{6,5\cdot 3^{2}}{100} = 5,52 kN.m/m$

Momento positivo (+) em Y:

$M_{y}^{+} = \mu_{y} \cdot \frac{p\cdot l_{x}^{2}}{100}$

$M_{y}^{+} = 2,43 \cdot \frac{6,5\cdot 3^{2}}{100} = 1,42 kN.m/m$

Momento negativo (-) em Y:

$M_{y}^{-} = \mu^{'}_{y} \cdot \frac{p\cdot l_{x}^{2}}{100}$

$M_{y}^{-} = 7,91 \cdot \frac{6,5\cdot 3^{2}}{100} = 4,63 kN.m/m$

A partir dos momentos fletores atuantes, é possível dimensionar as armaduras necessárias.

CONCLUSÃO

Apesar de existirem métodos mais sofisticados, disponíveis em ferramentas computacionais, a utilização das tabelas para dimensionamento de lajes maciças ainda é uma opção prática muito utilizada e com resultados satisfatórios, sendo suas grandes vantagens a facilidade de uso e verificação manual dos cálculos.

EXEMPLO 1

EXEMPLO 2

EXEMPLO 3

CONCLUSÃO

Posts relacionados

1 comentário em “DETERMINAÇÃO DE MOMENTOS EM LAJES MACIÇAS”