Desenvolvido pelo renomado engenheiro Karl Terzaghi, considerado o “pai da Mecânica dos Solos”, esse método teórico oferece uma abordagem prática e confiável para calcular a capacidade de carga de fundações superficiais (sapata). Baseando-se em dois parâmetros fundamentais do solo – o ângulo de atrito interno e a coesão –, o método de Terzaghi permite estimar com precisão a resistência do solo submetido ao carregamento de uma fundação superficial (sapata).
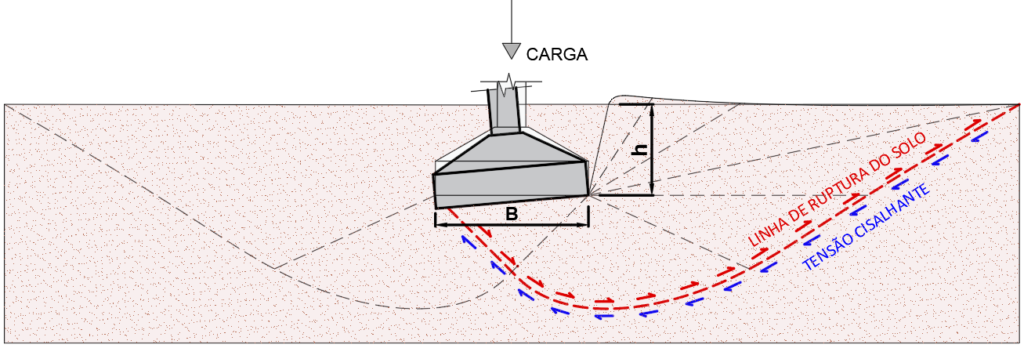
O método desenvolvido por Karl Terzaghi baseia-se na premissa de que a resistência do solo ao carregamento de uma fundação depende de três componentes principais:
- Resistência devido à coesão do solo;
- Resistência devido à fricção interna do solo (associada ao ângulo de atrito interno);
- Resistência devido ao peso próprio do solo acima da fundação.

Onde:
![]() Resistência Última do Solo
Resistência Última do Solo
![]() Coeficientes de Forma
Coeficientes de Forma
![]() Fatores de Capacidade de Carga (obtidos a partir do ângulo de atrito do solo)
Fatores de Capacidade de Carga (obtidos a partir do ângulo de atrito do solo)
![]() Coesão do Solo
Coesão do Solo
![]() Peso Específico do Solo
Peso Específico do Solo
![]() Largura da Fundação (Sapata)
Largura da Fundação (Sapata)
![]() Altura de Embutimento da Fundação (profundidade)
Altura de Embutimento da Fundação (profundidade)
MÉTODO DE TERZAGHI: EXEMPLO DE CÁLCULO
Para ilustrar a aplicação do Método de Terzaghi no dimensionamento de fundações superficiais (sapata), apresentaremos a resolução de um exemplo prático.
Considere as seguintes informações:
- Solo arenoso, compacto
- Coesão do solo: C = 4 kPa
- Ângulo de atrito do solo: Φ = 37°
- Profundidade de assentamento da fundação (embutimento): h = 1,5 m
- Peso específico do solo: γ = 1,8 tf/m³
- Largura da sapata: B = 1,0 m (sapata retangular)
1º PASSO: Modo de ruptura do solo
Com base na descrição do solo como arenoso compacto, pode-se deduzir que a densidade relativa está no intervalo de 70% a 85% (70% < Dr < 85%). Assim, espera-se que o tipo de ruptura seja generalizada.


Tudo o que foi apresentado até o momento sobre a teoria de Terzaghi se refere à ruptura generalizada. No caso de se considerar a ruptura local, os parâmetros do solo a serem adotados devem ser:
![]()
![]()
2º PASSO: Coeficientes de forma da sapata
O método proposto por Terzaghi foi originalmente desenvolvido para sapatas corridas, tendo sido posteriormente ajustado com a introdução de coeficientes específicos para sapatas quadradas / retangulares e circulares:

Portanto, para sapata retangular, temos:
![]()
![]()
![]()
3º PASSO: Fatores de Capacidade de Carga
Os fatores de capacidade de carga ![]() ,
, ![]() e
e ![]() podem ser obtidos pelo gráfico abaixo ou através da utilização de fórmulas:
podem ser obtidos pelo gráfico abaixo ou através da utilização de fórmulas:

![]()
![]()
![]()
![]()
Há outras equações disponíveis para o cálculo do fator ![]() , que tornam seu uso mais prático em planilhas e softwares, em comparação com o gráfico apresentado. Dentre as equações frequentemente empregadas, destacam-se:
, que tornam seu uso mais prático em planilhas e softwares, em comparação com o gráfico apresentado. Dentre as equações frequentemente empregadas, destacam-se:
![]() Meyerhof,
Meyerhof, ![]() em graus.
em graus.
![]() Davis e Booker,
Davis e Booker, ![]() em radianos (fundação lisa).
em radianos (fundação lisa).
![]() Davis e Booker,
Davis e Booker, ![]() em radianos (fundação rugosa).
em radianos (fundação rugosa).
![]() Ueno,
Ueno, ![]() em radianos (fundação lisa).
em radianos (fundação lisa).
Para valores de ![]() < 30° é possível utilizar quaisquer equações para
< 30° é possível utilizar quaisquer equações para ![]() , para valores superiores a 30° as diferenças entre os diferentes métodos aumentam.
, para valores superiores a 30° as diferenças entre os diferentes métodos aumentam.
Portanto:
![]()
![]()
![]()
![]()
4º PASSO: Cálculo da capacidade de carga do solo (tensão última)
Conforme proposto por Terzaghi para a determinação da tensão última do solo:

Portanto:

![]() kPa =
kPa = ![]() kg/cm²
kg/cm²
5º PASSO: Cálculo da tensão admissível do solo (Método Terzaghi)
Após calcular a tensão última do solo, que representa o valor limite capaz de levar o solo à ruptura, determinaremos a tensão admissível, correspondente à tensão de trabalho a ser utilizada no dimensionamento da sapata:
![]()
Para fundações superficiais, o Fator de Segurança adotado para determinar a tensão admissível é igual a 3, portanto:
![]() kg/cm²
kg/cm²
6º PASSO: Cálculo da carga máxima do pilar
Conhecida a tensão admissível do solo (![]() kg/cm²) e a menor dimensão da sapata, é possível determinar a carga máxima suportada pela sapata ao se definir o seu comprimento:
kg/cm²) e a menor dimensão da sapata, é possível determinar a carga máxima suportada pela sapata ao se definir o seu comprimento:
- Largura da sapata: B = 1,0 m = 100 cm (valor informado no cálculo da tensão última do solo)
- Comprimento da sapata: L = 2,0 m = 200 cm
![]()
![]()
Conforme o método de Terzaghi para determinar a tensão admissível do solo e dimensionar a sapata, a carga máxima transmitida pelo pilar à sapata especificada no exemplo é de 38 tf.
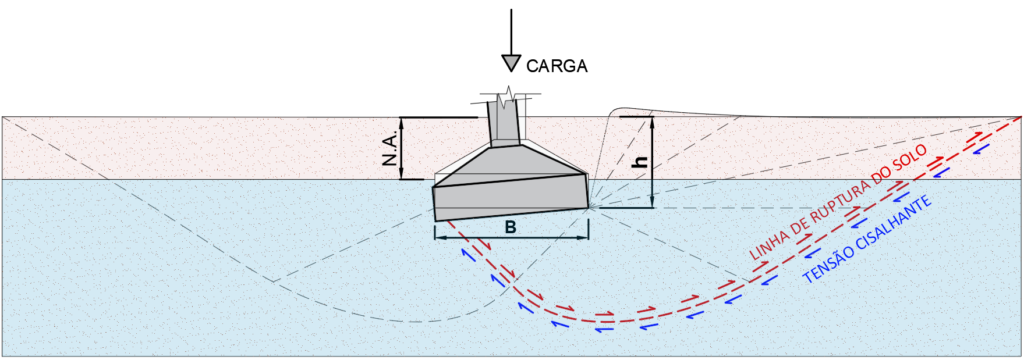
INFLUÊNCIA DO LENÇOL FREÁTICO EM SAPATAS
A influência do lençol freático deve ser considerada em duas situações possíveis:
- Nível d’água acima da base da fundação
- Nível d’água abaixo da fundação em uma profundidade até B, que equivale ao diâmetro ou menor lado


Para o Caso 1, deve-se realizar as seguintes alterações na fórmula original:
- calcular o termo
 como sendo
como sendo  (Sobrecarga)
(Sobrecarga) - utilizar
 no termo
no termo  (Atrito)
(Atrito)
Para o Caso 2, deve-se considerar:
- utilizar
 em
em  (Sobrecarga)
(Sobrecarga) - termo
 , calcular como
, calcular como  (Atrito)
(Atrito)
OUTROS MÉTODOS
Outro método bastante utilizado para a determinação da tensão admissível do solo e dimensionamento de sapata são os baseados no resultado do ensaio SPT. O site Estude Engenharia oferece ferramentas para determinar a tensão admissível a partir do SPT e dimensionamento geotécnico:

Pingback: ENSAIO DE CISALHAMENTO DIRETO DO SOLO - Estude Engenharia
Pingback: Planilha: Dimensionamento de Sapata (Método de Terzaghi) - Estude Engenharia
Pingback: Fundação Superficial: Tudo o que Você Precisa para Projetar - Estude Engenharia