Neste exercício, apresentado como EXEMPLO 5.3 no livro de ANÁLISE ESTRUTURAL do autor Aslam Kassimali, vamos analisar a viga isostática abaixo e traçar os diagramas de momento fletor e esforço cortante.

Utilizaremos o método das seções para definir as equações que determinam os esforços em cada segmento da viga.
PROCEDIMENTO DE CÁLCULO
1º PASSO: VERIFICAR GRAU HIPERESTÁTICO
Para que sejam determinadas as reações de apoio, devemos verificar o grau hiperestático da estrutura em questão. Sendo:
![]() número de reações de apoio (HA, VA e VB)
número de reações de apoio (HA, VA e VB)
![]() número de equações de equilíbrio
número de equações de equilíbrio
![]()
![]()
![]()
Temos, portanto, que o número de incógnitas (reações de apoio) é igual ao número de reações de equilíbrio. A estrutura é ESTATICAMENTE DETERMINADA EXTERNAMENTE.![]() grau hiperestático
grau hiperestático
Além disso, podemos perceber que a estrutura é ESTATICAMENTE ESTÁVEL EXTERNAMENTE pois os apoios promovem reações capazes de dar estabilidade à estrutura.
2º PASSO: DETERMINAR AS REAÇÕES DE APOIO

Utilizaremos as três equações de equilíbrio para determinar as reações nos apoios:
![]()
![]()
Não há cargas horizontais, portanto, a reação horizontal no apoio é igual a zero.
![]()
![]()
![]()
![]()
Para definir os valores respectivos de VA e VB, utilizaremos a 3ª equação de equilíbrio:
![]() Momento no ponto A
Momento no ponto A![]()
![]()
![]()
Sendo:![]()
Portanto:
![]()
![]()
3º PASSO: DETERMINAR OS ESFORÇOS SOLICITANTES
Para determinar os esforços solicitantes (cortante e momento) ao longo da viga, devemos analisar cada segmento separadamente. Os trechos são definidos sempre que há mudanças no carregamento e reações de apoio.
- SEÇÃO S1 (A – B):


![]() Eq. cortante
Eq. cortante![]() Eq. momento fletor
Eq. momento fletor
Note que o esforço cortante se mantém constante ao logo do trecho A-B pois a única carga vertical à esquerda da seção S1 é a reação de apoio em A.
![]()
O momento fletor, no entanto, varia de acordo com a distância da seção S1 analisada. Portanto, para os esforços à esquerda da seção S1:

- SEÇÃO S2 (B – C):


![]() Eq. cortante
Eq. cortante![]() Eq. momento fletor
Eq. momento fletor
Exatamente no ponto B, a cortante sofre alteração por conta da carga concentrada e se mantém constante.
![]()
A força concentrada de 265 kN causa momento fletor na seção S2, mas devemos estar atentos à distância entre essa força e a seção em análise: (x-3)

- SEÇÃO S3 (C – D):


![]() Eq. cortante
Eq. cortante![]() Eq. momento fletor
Eq. momento fletor
Conforme a seção S3 avança, de C para D, o esforço cortante recebe a adição contínua de carga (carga distribuída). Dessa forma, a variação de carga entre C e D será linear.

Exatamente no ponto C atua um momento fletor pontual com valor de -245 kN (negativo, sentido anti-horário), gerando uma descontinuidade no gráfico conforme veremos mais adiante. Devemos estar atento ao fato de existir um carregamento uniformemente distribuído, com carga equivalente de ![]() e distância de atuação na seção S3 igual a
e distância de atuação na seção S3 igual a ![]() .
.

- SEÇÃO S4 (D – E):

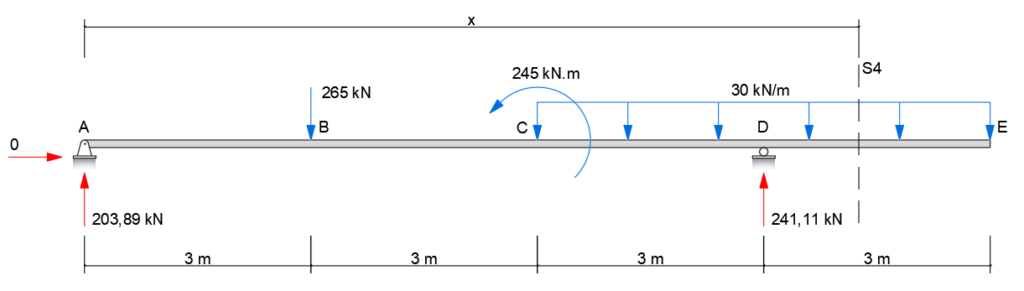
![]() Eq. cortante
Eq. cortante![]() Eq. momento fletor
Eq. momento fletor
No ponto D, onde há um apoio e reação vertical igual a 241,11 kN, há uma descontinuidade no valor do esforço cortante:

A reação de apoio em D, com valor de 241,11 kN, causa momento fletor na seção S4. Devemos estar atentos à distância entre essa força e a seção em análise: (x-9)

4º PASSO: DESENHAR OS GRÁFICOS DE ESFORÇO CORTANTE E MOMENTO FLETOR
- ESFORÇO CORTANTE:

Para traçar o diagrama de esforço cortante basta ligar os pontos com os valores calculados anteriormente, devendo estar atento às descontinuidades provocadas por cargas pontuais e a forma como a carga distribuída se apresenta no gráfico.
Note que a expressão que determina o esforço cortante em qualquer seção do trecho C-D é uma equação de 1º grau, portanto, o trecho será formado por uma reta inclinada.
![]() Eq. cortante
Eq. cortante
- MOMENTO FLETOR:

Como já calculamos os valores do momento fletor atuante em diferentes seções da viga, basta ligar os pontos. A atenção se faz necessária no ponto onde existe a atuação de um momento fletor pontual.
Nos trechos onde existe a atuação de carga uniformemente distribuída (C-D e D-E), o gráfico apresenta forma de parábola. Note que a expressão que determina o momento fletor atuante em qualquer seção do trecho C-D, por exemplo, é uma equação de 2º grau:
![]() Eq. momento fletor
Eq. momento fletor
Podemos calcular a profundidade do vértice da seguinte forma:
![]()
Além disso, podemos utilizar a equação de momento do trecho C-D e descobrir em que ponto o gráfico toca o eixo (momento igual a zero):
![]()
![]()
![]()
![]()
Portanto, para o encontrar o valor de x onde o momento fletor é igual a zero:
![]()
Resolvendo a equação de 2º grau:
![]()
![]()
![]()
REFERÊNCIA BIBLIOGRÁFICA
Análise Estrutural

