ISOSTÁTICA: EXERCÍCIO 5.8 - Estude Engenharia

Neste exercício, apresentado como EXEMPLO 5.8 no livro de ANÁLISE ESTRUTURAL do autor Aslam Kassimali, vamos analisar a viga isostática abaixo e traçar os diagramas de momento fletor e esforço cortante.

Utilizaremos o método das seções para definir as equações que determinam os esforços em cada segmento da viga.

PROCEDIMENTO DE CÁLCULO: EXERCÍCIO ISOSTÁTICA

1º PASSO: VERIFICAR GRAU HIPERESTÁTICO

Para que sejam determinadas as reações de apoio, devemos verificar o grau hiperestático da estrutura em questão. Sendo:

$r = 3 \rightarrow$ número de reações de apoio (HA, VA e VB)

$e = 3 \rightarrow$ número de equações de equilíbrio

$\sum F_{h} = 0$

$\sum F_{v} = 0$

$\sum M = 0$

Temos, portanto, que o número de incógnitas (reações de apoio) é igual ao número de reações de equilíbrio. A estrutura é ESTATICAMENTE DETERMINADA EXTERNAMENTE.
$i_{e} = r - e = 3 - 3 = 0 \rightarrow$ grau hiperestático

Além disso, podemos perceber que a estrutura é ESTATICAMENTE ESTÁVEL EXTERNAMENTE pois os apoios promovem reações capazes de dar estabilidade à estrutura.

2º PASSO: DETERMINAR AS REAÇÕES DE APOIO

Utilizaremos as três equações de equilíbrio para determinar as reações nos apoios:

$\sum F_{h} = 0$

$HB = 0$

Não há cargas horizontais, portanto, a reação horizontal no apoio é igual a zero.

$\sum F_{v} = 0$

$VB + VC - \frac{(45\times 4)}{2} - (45\times 6,5) - \frac{(45\times 2)}{2} = 0$

$VB + VC - 90 - 292,5 - 45 = 0$

$VB + VC = 427,5 kN$

Para definir os valores respectivos de VB e VC, utilizaremos a 3ª equação de equilíbrio:

$\circlearrowleft^{+} \sum M _{B} = 0 \rightarrow$ Momento no ponto B

$\left ( \frac{45 \times 4}{2} \right ) \times \frac{4}{3} - (45 \times 6,5)\times \frac{6,5}{2} + VC\times 6,5 - \left ( \frac{45 \times 2}{2} \right ) \times \left ( 6,5 + \frac{2}{3} \right ) = 0$

$120 - 950,625 + VC\times 6,5 - 322,5 = 0$

$VC = \frac{1.153,125}{6,5} = 177,4 kN$

Sendo:
$VB + VC = 427,5 kN$

Portanto:

$VB + 177,4 = 427,5 kN$

$VB = 250,1 kN$

3º PASSO: DETERMINAR OS ESFORÇOS SOLICITANTES

Para determinar os esforços solicitantes (cortante e momento) ao longo da viga, devemos analisar cada segmento separadamente. Os trechos são definidos sempre que há mudanças no carregamento e reações de apoio.

SEÇÃO S1 (A – B): $0 \leq x \leq 4$

$V_{S1} = - \frac{1}{2} \times \frac{45\times x}{4} \times x \rightarrow$ Eq. cortante

$M_{S1} = - \frac{1}{2} \times \frac{45\times x}{4} \times x \times \frac{x}{3} \rightarrow$ Eq. momento fletor

No caso de carregamento triangular, conforme a seção S1 avança a uma distância x, a carga considerada é igual a $\frac{qx}{l}$ .

$V_{S1} = - \frac{1}{2} \times \frac{45\times x}{4} \times x \begin{cases}\frac{1}{2} \times \frac{45\times 0}{4} \times 0 = 0 & \text{ se } x= 0\\\frac{1}{2} \times \frac{45\times 4}{4} \times 4 = -90 kN & \text{ se } x=4\end{cases}$

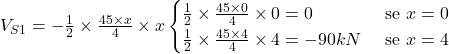
Além disso, podemos notar que se trata de uma equação de 2º grau e o gráfico do esforço cortante será em forma de parábola para esse tipo de carregamento. Calculando o valor da cortante para o centro de carga, ou seja, para x = 2/3 do comprimento:

$V_{S1} = - \frac{1}{2} \times \frac{45\times \left ( \frac{2}{3} \times 4 \right )}{4} \times \left ( \frac{2}{3} \times 4 \right ) = -40 kN$

Para o cálculo do momento fletor, também é necessário estar atento à consideração da carga $\frac{qx}{l}$ e a sua atuação a 1/3 da seção S1 considerada (substituição por carga equivalente $\frac{ql}{2}$ ).

$M_{S1} = - \frac{1}{2} \times \frac{45\times x}{4} \times x \times \frac{x}{3}\begin{cases}\frac{1}{2} \times \frac{45\times 0}{4} \times 0 \times \frac{0}{3} = 0 & \text{ se } x= 0\\\frac{1}{2} \times \frac{45\times 4}{4} \times 4 \times \frac{4}{3} = -120 kN.m & \text{ se } x= 4\end{cases}$

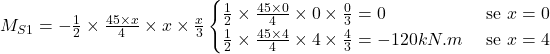
Além disso, podemos calcular o momento atuante onde se encontra o centro de carga, ou seja, para x = 2/3 do comprimento:

$M_{S1} = - \frac{1}{2} \times \frac{45\times \left ( \frac{2}{3}\times 4 \right )}{4} \times \left ( \frac{2}{3}\times 4 \right ) \times \frac{\left ( \frac{2}{3}\times 4 \right )}{3} = -35,55kN.m$

SEÇÃO S2 (B – C): $4 \leq x \leq 10,5$

$V_{S2} = - \frac{45\times 4}{2} + 250,1 - 45 \times (x -4) \rightarrow$ Eq. cortante

$M_{S2} = - \frac{45\times 4}{2} \times \left ( x - \frac{2}{3} \times 4 \right ) + 250,1 \times (x - 4) - 45 \times (x-4) \times \frac{x-4}{2} \rightarrow$ Eq. momento fletor

No ponto B, onde há um apoio e reação vertical igual a 250,1 kN, há uma descontinuidade no valor do esforço cortante. E, conforme a seção S2 avança de B para C, o esforço cortante recebe a adição contínua de carga (carga distribuída). Dessa forma, a variação de carga entre B e C será linear.

$V_{S2} = \begin{cases} V_{S2} =- \frac{45\times 4}{2} + 250,1 - 45 \times (4 -4) = 160,1kN & \text{ se } x= 4 \\ V_{S2} = - \frac{45\times 4}{2} + 250,1 - 45 \times (10,5 -4) = - 132,4kN & \text{se } x= 10,5\end{cases}$

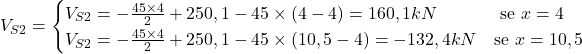
Para a análise do momento fletor na seção S2, trecho B-C, observar que a distância de atuação da carga triangular do trecho A-B para a seção é igual a $\left ( x - \frac{2}{3} \times 4 \right )$ . Portanto:

$M_{S2} = \begin{cases}\frac{45\times 4}{2} \times \left ( 4 - \frac{2}{3} \times 4 \right ) + 250,1 \times (4 - 4) - 45 \times (4-4) \times \frac{4-4}{2} = -120 kN.m & \text{ se } x= 4 \\ \frac{45\times 4}{2} \times \left ( 10,5 - \frac{2}{3} \times 4 \right ) + 250,1 \times (10,5 - 4) - 45\times (10,5-4) \times \frac{10,5-4}{2} = -29,975 kN.m & \text{ se } x= 10,5\end{cases}$

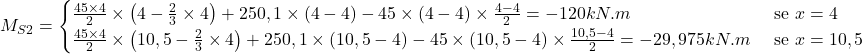
SEÇÃO S3 (C – D): $10,5 \leq x \leq 12,5$

$V_{S3} = - \frac{45\times 4}{2} + 250,1 - 45 \times 6,5 + 177,4 - \frac{\left { 45 - \frac{45 \times (12,5 - x)}{2}\ \right }\times \left ( x -10,5 \right )}{2} \rightarrow$ Eq. cortante

No entanto, torna-se mais fácil trabalhar com as forças atuantes “da direita para a esquerda”:

Dessa forma, só é necessário analisar o carregamento triangular presente no trecho C-D:

Portanto: $0 \leq x \leq 2$

$V_{S3} = + \frac{1}{2} \times \frac{45\times x}{2} \times x \rightarrow$ Eq. cortante

Note que o sinal agora é positivo pois estamos analisando as forças “da direita para a esquerda”. Segundo a convenção de sinais adotada, a força cortante é positiva quando a seção à esquerda tende a subir em relação a face oposta ou quando a seção à esquerda tende a descer.

$V_{S3} = + \frac{1}{2} \times \frac{45\times x}{2} \times x \begin{cases}\frac{1}{2} \times \frac{45\times 0}{2} \times 0 = 0 & \text{ se } x= 0 \\ \frac{1}{2} \times \frac{45\times 2}{2} \times 2 = 45 kN & \text{ se } x= 2 \end{cases}$

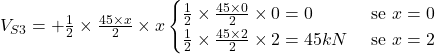
A diferença entre o valor da cortante obtida ao final do trecho B-C (-132,4 kN) e o valor obtido ao final do trecho D-C (45 kN) é o valor da reação de apoio em C (177,4 kN).

Podemos, ainda, calcular o valor do esforço cortante à 2/3 do início da seção S3:

$V_{S3} = + \frac{1}{2} \times \frac{45\times \left ( \frac{2}{3} \times 2 \right )}{2} \times \left ( \frac{2}{3} \times 2 \right ) = 20 kN$

Utilizaremos o mesmo artifício para facilitar o cálculo do momento fletor: analisar as forças “da direita para a esquerda”.

$M_{S3} = - \frac{1}{2} \times \frac{45\times x}{2} \times x \times \frac{x}{3} \rightarrow$ Eq. momento fletor

Portanto: $0 \leq x \leq 2$

$M_{S3} = - \frac{1}{2} \times \frac{45\times x}{2} \times x \times \frac{x}{3}\begin{cases} - \frac{1}{2} \times \frac{45\times 0}{2} \times 0 \times \frac{0}{3} = 0 & \text{ se } x= 0 \\ - \frac{1}{2} \times \frac{45\times 2}{2} \times 2 \times \frac{2}{3} = - 30 kN.m & \text{ se } x= 2\end{cases}$

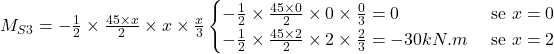
Calculando o valor do momento fletor à 2/3 do início da seção S3:

$M_{S3} = - \frac{1}{2} \times \frac{45\times \left ( \frac{2}{3} \times 2 \right )}{2} \times\left ( \frac{2}{3} \times 2 \right ) \times \frac{\left ( \frac{2}{3} \times 2 \right )}{3} \cong - 8,89 kN.m$

4º PASSO: DESENHAR OS GRÁFICOS DE ESFORÇO CORTANTE E MOMENTO FLETOR

ESFORÇO CORTANTE:

Para traçar o diagrama de esforço cortante basta ligar os pontos com os valores calculados anteriormente, devendo estar atento às descontinuidades provocadas por cargas pontuais e a forma como a carga distribuída se apresenta no gráfico.

Note que a expressão que determina o esforço cortante em qualquer seção dos trechos A-B e C-D é uma equação de 2º grau, portanto, o gráfico é formado por uma parábola.

Além disso, podemos calcular a distância onde a cortante tem valor igual a zero no trecho B-C.

$V_{S2} = - \frac{45\times 4}{2} + 250,1 - 45 \times (x -4) \rightarrow$ Eq. cortante

$0 = - \frac{45\times 4}{2} + 250,1 - 45 \times (x -4)$

$0 = - 90 + 250,1 - 45x + 180$

$x = \frac{340,1}{45} \cong 7.55 m$

A distância está em relação ao ponto A, portanto, o valor da cortante igual a zero está a 3,55m do apoio em B.

MOMENTO FLETOR:

Como já calculamos os valores do momento fletor atuante em diferentes seções da viga, basta ligar os pontos.

O máximo valor positivo pode ser encontrado a partir da equação do momento fletor do trecho B-C utilizando o valor de x no qual cortante é igual a zero (onde a cortante cruza o eixo y, o momento fletor é máximo).

$M_{S2} = - \frac{45\times 4}{2} \times \left ( x - \frac{2}{3} \times 4 \right ) + 250,1 \times (x - 4) - 45 \times (x-4) \times \frac{x-4}{2} \rightarrow$ Eq. momento fletor

$M_{S2} = - \frac{45\times 4}{2} \times \left ( 7,55 - \frac{2}{3} \times 4 \right ) + 250,1 \times (7,55 - 4) - 45 \times (7,55-4) \times \frac{7,55-4}{2}$

$M_{S2} = -440,13 + 889,60 - 284,67 = 164,80 kN.m$

REFERÊNCIA BIBLIOGRÁFICA

O exercício de viga isostática apresentado foi extraído do livro: