ESTAQUEAMENTO: BLOCO SOBRE DUAS ESTACAS

UTILIZE A PLANILHA ON-LINE PARA CÁLCULO DE ESTAQUEAMENTO (ESTACAS EM GRUPO)

Em post anterior, explicamos o que é o cálculo de estaqueamento e como funciona a ferramenta disponibilizada no site. Agora, vamos demonstrar os cálculos realizados através do método geral para o estaqueamento de um bloco sobre duas estacas e verificar a eficiência de grupo pelo método de Feld.

BLOCO SOBRE DUAS ESTACAS

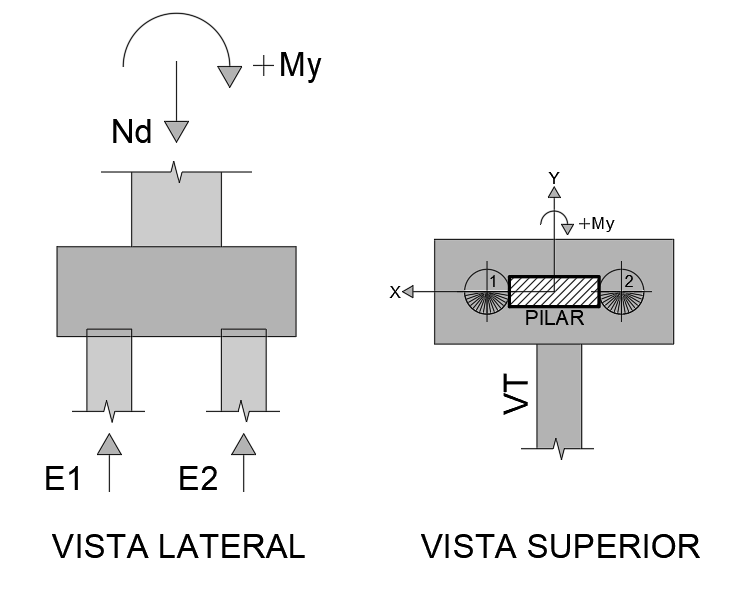
Para demonstrar os cálculos, considerar os seguintes valores:

  • Espaçamento entre as estacas (e) – cm: 90
  • Carga que chega do pilar (Nd) – tf: 50
  • Momento que chega do pilar (My) – tf.m: 4
  • Capacidade de carga geotécnica de cada estaca – tf: 30

O primeiro ponto que devemos observar é que o bloco sobre duas estacas só possibilita a transferência de momento pelo binário de reações em seu eixo Y. Para resolver a transferência de momento segundo o eixo X e promover rigidez ao conjunto, há de se prever uma viga de travamento (VT) ou realizar o dimensionamento e verificação das estacas submetidas aos esforços transversais.

ESTAQUEAMENTO

Através do método geral, faremos as verificações dos cálculos:

P _{i} = \frac{R}{n} \pm \frac{M _{y}\times x_{i}}{\sum x_{i}^{2}} \pm \frac{M _{x}\times y_{i}}{\sum y_{i}^{2}}

Como não há transferência de momento em X ou excentricidades em Y, podemos desconsiderar a terceira parcela da fórmula.

O valor de xi (excentricicade entre o centro do pilar e a estaca em questão) é, portanto, espaçamento / 2 = 0.9 / 2 = 0.45.

P _{E1} = \frac{50}{2} - \frac{4 \times 0.45}{0.405} = 25 - 4.44 = 20.56 tf

P _{E2} = \frac{50}{2} + \frac{4 \times 0.45}{0.405} = 25 + 4.44 = 29.44 tf

Como o momento em Y tende a modificar o centro de aplicação de carga, as estacas terão reações distintas.

Apesar dos métodos menos sofisticados estarem sujeitos a críticas por suas hipóteses simplificadoras, a experiência mostra que o estaqueamento projetado dessa forma se comporta de maneira satisfatória e, de algum modo, a favor da segurança. Quando se analisa o mesmo estaqueamento projetado por um método simplista e outro método que considere a contenção lateral do solo e condição de engaste no bloco de coroamento, percebe-se que a diferença de carga axial entre as estacas é maior no primeiro caso, direcionando a um dimensionamento geotécnico mais conservador se comparado aos métodos sofisticados. Por outro lado, quando se considera a condição de engaste no bloco e a atuação de esforços transversais com contenção lateral do solo, obtém-se informações mais realistas sobre momentos fletores atuantes nas estacas para o dimensionamento a flexão.

CÁLCULO DE ESTAQUEAMENTO

EFICIÊNCIA DE GRUPO

\varepsilon = 1 - \frac{n_{1}\times \varepsilon_{1} + n_{2}\times \varepsilon_{2} + … n_{m}\times \varepsilon_{m}}{n_{1} + n_{2} + … n_{m}}

Feld apresenta uma regra simples para a consideração da eficiência de cada estaca em grupo: para cada estaca adjacente à estaca em análise, desconta-se 1/16 de sua eficiência. O método não leva em conta o espaçamento entre as estacas, no entanto, apresenta bons resultados para espaçamentos ≥ 2,5D.

Vamos verificar a eficiência partindo da informação da capacidade geotécnica de cada estaca = 30 tf.

\varepsilon_{1} = \varepsilon_{2} = 1 - \frac{1}{16} = 0.9375

E{1} = E{2} = 0.9375 \times 30 = 28.125 tf

\varepsilon_{g} = 1 - \frac{2 \times\frac{1}{16} }{2} = 0.9375 = 93.75\%

A capacidade de carga do grupo de estacas é, portanto, 93.75% da soma da capacidade de carga geotécnica (30 tf + 30 tf), 56.25 tf. É importante avaliar se a carga aplicada pelo pilar é inferior à capacidade de grupo considerando a perda de eficiência.

Outra observação importante é se alguma das estacas, considerando a perda de eficiência, tem a sua capacidade de carga inferior à solicitação calculada no estaqueamento. No exemplo em questão, a capacidade de carga real da estaca E2 é de 28.125 tf, valor um pouco inferior à carga solicitante de 29.44 tf obtida no estaqueamento.

REFERÊNCIAS BIBLIOGRÁFICAS

Elementos de Fundações em Concreto

Fundações em Estacas

Mecânica dos Solos – Obras de Terra e Fundações

Posts relacionados

Rolar para cima