LAJE TRELIÇADA: PROCEDIMENTO DE CÁLCULO – PARTE 2

UTILIZE A PLANILHA ON-LINE PARA DIMENSIONAMENTO DE LAJE TRELIÇADA

PLANILHA PARA DIMENSIONAMENTO DE LAJE TRELIÇADA

O sistema construtivo de lajes treliçadas, que utiliza vigotas pré-moldadas com armação em formato de treliça e algum elemento de enchimento (EPS, bloco cerâmico…) para reduzir o consumo de concreto onde o mesmo não trabalha, é o mais utilizado no Brasil em obras residenciais. Por isso, faremos uma série de posts para demonstrar todo o procedimento de cálculo e verificações que se fazem necessárias.

LAJE TRELIÇADA: PROCEDIMENTO DE CÁLCULO – PARTE 1
LAJE TRELIÇADA: PROCEDIMENTO DE CÁLCULO – PARTE 2
LAJE TRELIÇADA: PROCEDIMENTO DE CÁLCULO – PARTE 3
LAJE TRELIÇADA: PROCEDIMENTO DE CÁLCULO – PARTE 4

INFORMAÇÕES DE CÁLCULO

Primeiramente, vamos definir as informações necessárias para todo o procedimento de cálculo. Serão adotados os seguintes valores:

COMPRIMENTO / VÃO DA LAJE: 400 cm

BASE DA VIGOTA: 12 cm

TIPO DE ENCHIMENTO: EPS (H12/40)

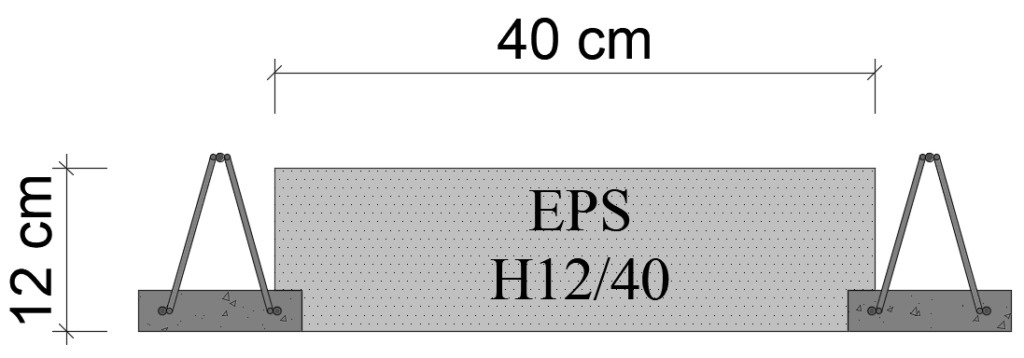
TRELIÇA: TR 12646

ESPESSURA DE CAPA: 5 cm

ARMADURA ADICIONAL: 1 Φ 8 mm

CONCRETO: 25 MPa
CARGA PERMANENTE: 100 kg/m² (Contrapiso + revestimento)
CARGA ACIDENTAL: 150 kg/m²

PROCEDIMENTO DE CÁLCULO

ALTURA ÚTIL – d (cm)

Entende-se como altura útil a distância entre o centro de gravidade das armaduras longitudinais tracionadas e a fibra mais comprimida do concreto.

$A_{s} = 0,566 cm^{2} \rightarrow$ Área de aço da treliça, 2 Φ 6 mm

$A_{s,adc } = 0,502 cm^{2} \rightarrow$ Área de aço da adicional, 1 Φ 8 mm

Considerando o cobrimento c = 1,5 cm e a presença de uma armadura adicional Φ 8 mm (diâmetro diferente dos fios inferiores da treliça), podemos calcular d’ como:

$d' = \frac{2\times A_{s}\times y_{cg1} + A_{s,adc}\times y_{cg2} }{A_{s} + A_{s,adc}}$

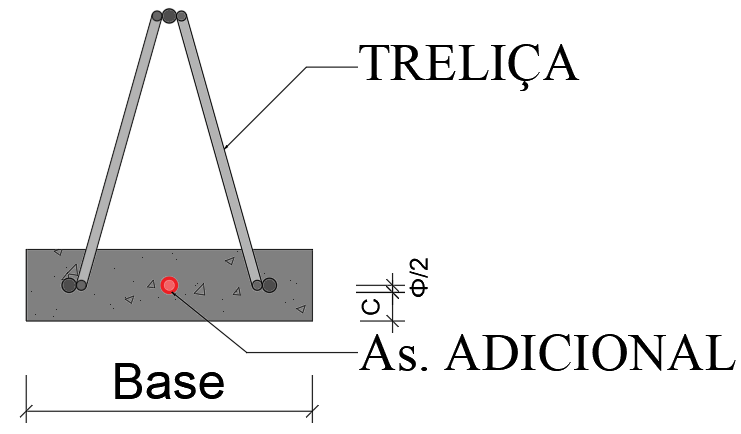
Portanto: $d' = \frac{2\times 0,283\times \left ( 1,5 + \frac{0,6}{2} \right ) + 0,502\times \left ( 1,5 + \frac{0,8}{2}\right ) }{0,566 + 0,502} = 1,847 cm$

A altura da laje treliçada é igual a 17 cm ( $\beta 17$ ), pois: $h = He + C = 12cm + 5cm = 17cm$

Temos que a altura útil (d) é, portanto:

$d = h - d' = 17 - 1,847 \cong 15,153cm$

PROFUNDIDADE DA LINHA NEUTRA – LN

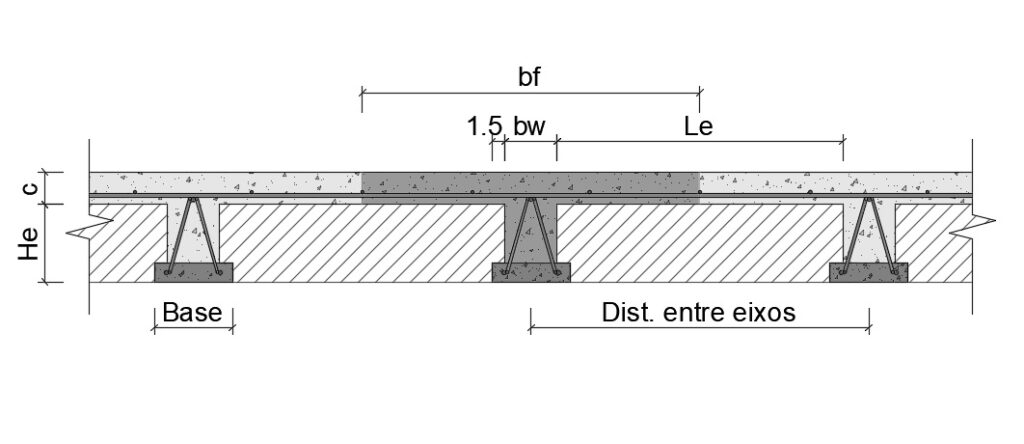
Para a verificação da profundidade da Linha Neutra – LN, utiliza-se a fórmula a seguir:

$x = \frac{0,68\cdot d \pm \sqrt{\left ( 0,68d \right )^{2} - 4\cdot 0,272\left ( \frac{M_{d}}{b_{w\cdot f_{cd}}} \right )}}{0,544}$

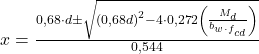
E importante destacar que, em lajes nervuradas, é uma boa prática trabalhar com a Linha Neutra dentro da espessura da capa, apesar de ser possível trabalhar com parte da alma (bw) ajudando nas solicitações de compressão da seção.

$M_{d} = M_{k} \times 1,4 = 4,23 \times 1,4 = 5,922 kN.m \rightarrow$ Momento atuante de cálculo

Portanto:

$x = \frac{0,68\cdot 0,15153 \pm \sqrt{\left ( 0,68\cdot 0,15153 \right )^{2} - 4\cdot 0,272\left ( \frac{5,922}{0,49\cdot \frac{25\cdot 10^{3}}{1,4}} \right )}}{0,544}$

OBSERVAÇÃO: Por definição, o termo Bw representa a largura da região comprimida da peça. No caso da laje treliçada, considera-se a capa de concreto como mesa colaborante, adotando-se, portanto, Bf = 49 cm.

$x = \frac{0,1030 \pm 0,0994}{0,544}$

$x_{1} = \frac{0,1030 + 0,0994}{0,544} = 0,3720 m = 37,2 cm \rightarrow$ LN fora da seção (incorreto)

$x_{2} = \frac{0,1030 - 0,0994}{0,544} = 0,0066 m = 0,66 cm$

A profundidade da Linha Neutra é $x = 0,66 cm$

$\frac{x}{d} = \frac{0,66}{15,153} = 0,0435 \rightarrow$ Domínio 2

ÁREA DE AÇO (ELU) – As

Primeiramente, calcula-se o braço de alavanca (z), dado por:

$z = d - 0,4\cdot x = 15,153 - 0,4 \cdot 0,66 = 14,889 cm$

Agora, podemos calcular a área de aço:

$A_{s} = \frac{M_{d}}{z\cdot f_{yd}}$ , sendo $f_{yd} = \frac{f_{yk}}{1,15}$

Para o aço CA-60, temos que $f_{yk} = 600 MPa = 60 kN/cm^{2}$

$A_{s} = \frac{5,922 kN.m}{0,14889 m\cdot \frac{60kN/cm^{2}}{1,15}} = 0,762 cm^{2}$

Temos que, para atender ao Estado Limite Último – ELU, é necessária uma área de aço $A_{s} = 0,762 cm^{2}$ . Considerando a armadura da treliça TR 12646 (2 Φ 6 mm) com área de aço $A_{s} = 0,566 cm^{2}$ mais a armadura adicional (1 Φ 8 mm) $A_{s,adc } = 0,502 cm^{2}$ , temos uma área de aço total de:

$A_{s,tot} = 0,566 + 0,502 = 1,068 cm^{2}$

Portanto, está garantida uma área de aço adotada maior (ou igual) que a área de aço calculada. $A_{s,tot} \geq A_{s}$

VERIFICAÇÃO AO CISALHAMENTO

Para prescindir o uso de armadura transversal para resistir aos esforços de tração devido à força cortante, é necessário que a força solicitante de cálculo seja menor ou igual à resistência de projeto ao cisalhamento:

$V_{Sd} \leq V_{Rd1} = \left [ \tau_{Rd} \cdot k \cdot (1,2 + 40\cdot \rho_{1}) \right ] \cdot b_{w}\cdot d$

Onde:

$\tau_{Rd} = 0,25 \cdot f_{ctd} = 0,25 \cdot \frac{f_{ctk,inf}}{\gamma _{c}} \rightarrow$ Tensão resistente de cálculo ao cisalhamento

$f_{ctk,inf} = 0,7 \cdot f_{ct,m}$ , sendo $f_{ct,m} = 0,3 \cdot f_{ck} ^{2/3}$

$\rho_{1}= \frac{A_{s1}}{b_{w}\cdot d} \leq 0,02$

$k = \left | 1,6 - d \right | \rightarrow$ d em metros

Além disso, é preciso verificar a compressão diagonal do concreto (bielas comprimidas):

$V_{Sd} \leq V_{Rd2} = 0,27 \cdot \alpha_{v2} \cdot f_{cd}\cdot b_{w}\cdot d$

Sendo:

$\alpha_{v2} = 1 - \frac{f_{ck}}{250} \rightarrow$ $f_{ck}$ em MPa

Como calculado no post anterior, temos que a força cortante por nervura (valor característico) é $V_{k} = 4,23 kN$

O esforço cortante de cálculo é, portanto: $V_{d} = V_{k} \cdot 1,4 = 4,23 \cdot 1,4 = 5,922 kN$

CÁLCULOS:

$f_{ct,m} = 0,3 \cdot f_{ck} ^{2/3} = 0,3 \cdot 25^{2/3} = 2,654 MPa$

$f_{ctk,inf} = 0,7 \cdot 2,654 = 1,795MPa$

$\tau_{Rd} = 0,25 \cdot \frac{1,795}{1,4} = 0,32 MPa = 320 KPa$

$\rho_{1}= \frac{1,068}{9\cdot 15,153} = 0,0078 \leq 0,02$

$k = \left | 1,6 - 0,15153 \right | = 1,448$

Portanto:

$V_{Rd1} = \left [ \tau_{Rd} \cdot k \cdot (1,2 + 40\cdot \rho_{1}) \right ] \cdot b_{w}\cdot d$

$V_{Rd1} = \left [ 320 \cdot 1,448 \cdot (1,2 + 40\cdot 0,0078) \right ] \cdot 0,09 \cdot 0,15153 \cong 9,5 kN$

Verificamos que $V_{Sd} \left ( 5,922 kN \right ) \leq V_{Rd1} \left ( 9,5 kN \right )$ , é dispensável o uso de armadura contra o cisalhamento.

Verificando a biela de compressão:

$\alpha_{v2} = 1 - \frac{f_{ck}}{250} = 1 - \frac{25}{250} = 0,9$

$V_{Rd2} = 0,27 \cdot \alpha_{v2} \cdot f_{cd}\cdot b_{w}\cdot d$

$V_{Rd2} = 0,27 \cdot 0,9 \cdot \frac{25\cdot 10^{3}KPa}{1,4}\cdot 0,09\cdot 0,15153 = 59,17 kN$

CONCLUSÃO

Determinamos nesta segunda parte a área de aço necessária para o atendimento ao Estado Limite Último – ELU e verificamos as nervuras quanto aos esforços de cisalhamento, não sendo necessária armadura para combater esses esforços. A seguir, faremos a verificação das deformações no Estado Limite de Serviço – ELS, considerando a fissuração e fluência do concreto. Acompanhe todo o procedimento de cálculo nos próximos posts!

REFERÊNCIAS BIBLIOGRÁFICAS

Cálculo e detalhamento de estruturas usuais de concreto armado

MANUAL TÉCNICO DE LAJES TRELIÇADAS (ArcelorMittal)

Pingback: LAJE TRELIÇADA: PROCEDIMENTO DE CÁLCULO - PARTE 1 -

Pingback: LAJE TRELIÇADA: PROCEDIMENTO DE CÁLCULO – PARTE 3 -

Pingback: LAJE TRELIÇADA: PROCEDIMENTO DE CÁLCULO – PARTE 4 -

Pingback: PLANILHA PARA DIMENSIONAMENTO DE LAJE TRELIÇADA -

Pingback: CÁLCULO DE LAJES TRELIÇADAS -

Antonio

17 de outubro de 2025 em 12:38

Boa tarde,
Primeiramente lhe agradecer pelo conteúdo muito legal, bem feito e explicado.
Ficou uma dúvida no cálculo da Altura Útil, a variável Ycg não foi dito de onde vem ou como chegar, apenas apresentado que corresponde a (1,5+0,6/2), você conseguiria explicar por gentileza?

Responder

Engenheiro Civil - Felipe
17 de outubro de 2025 em 14:04
Olá, Antônio!
Agradeço muito pelo seu feedback. Esses valores correspondem à distância entre a fibra mais tracionada (na base da vigota) e o centro de gravidade da armadura.
Adicionei uma nova imagem ao texto para deixar essa relação mais clara. Espero que ajude na compreensão!
Abraço,
Felipe Queiroz
Responder
1. Antonio
  20 de outubro de 2025 em 12:43
  Muito obrigado, ajudou muito!
  Responder

20 de outubro de 2025 em 13:00

Professor Felipe, uma outra dúvida, no cálculo de profundidade da linha neutra, a fórmula de X, tem a parte:
(Md / (Bw * Fcd)).
Md = 5,922 (que fizemos no cálculo anterior)
Bw = 0,49 (fiquei com dúvida aqui, pois lá no começo eu tinha como 9cm)
Fcd = (25*10³)/1,4 (onde que buscamos esse número?)

Engenheiro Civil - Felipe
20 de outubro de 2025 em 13:30
Olá, Antônio!
Esclarecendo a sua dúvida: na fórmula original (também utilizada no cálculo de vigas de seção retangular), o termo Bw representa a largura da peça comprimida.
No caso da laje treliçada, a região comprimida corresponde à capa de concreto, que atua como mesa colaborante, com largura de 49 cm (0,49 m).
Por esse motivo, utilizei o termo Bf para representar essa largura, embora tenha mantido a fórmula com sua notação original.
Vou ajustar o texto para deixar essa explicação mais clara.
Agradeço muito pelo feedback — sua dúvida certamente pode ajudar outros leitores também!
Abraço,
Felipe Queiroz
Responder

20 de outubro de 2025 em 15:02

Perfeito Felipe, e no caso do Fcd, onde que buscamos esse número?
Na formula representa:
Fcd = (25*10³)/1,4

Engenheiro Civil - Felipe
20 de outubro de 2025 em 15:25
O Fcd representa a resistência de cálculo do concreto. O valor de 25 MPa corresponde à resistência característica (fck), e o fator 1,4 é o coeficiente de minoração da resistência do concreto (definido pela norma ABNT NBR 6118).
A conversão de 25 MPa para kPa (ou kN/m²) é feita multiplicando por 10³, garantindo a compatibilidade de unidades, já que o momento de cálculo (Md) está expresso em kN·m.
Responder
1. Antonio
  20 de outubro de 2025 em 16:29
  Excelente! Muito obrigado pelas orientações Felipe!
  Responder

LAJE TRELIÇADA: PROCEDIMENTO DE CÁLCULO – PARTE 2

UTILIZE A PLANILHA ON-LINE PARA DIMENSIONAMENTO DE LAJE TRELIÇADA

INFORMAÇÕES DE CÁLCULO